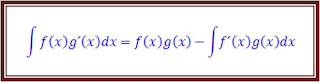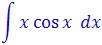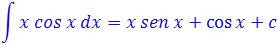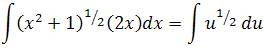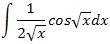¡Integrando con Paco!

miércoles, 29 de agosto de 2007

Sesión 3

3.2 Integración por partes
¡Cordial saludo Paco!
En esta sesión vamos a trabajar con una técnica de integración muy interesante, “la integración por partes”.
P. Creo saber porque dice que es interesante. Algunos amigos que ya cursaron cálculo integral, me dijeron que es la técnica que más problemas les causó.
Lo de interesante se confunde con la complejidad. En realidad el método que vamos a explorar es sencillo, sólo que algunas soluciones de integrales obligan a utilizar tanto este método como los anteriores. Es decir, en una integral es posible que se tenga que recurrir al método por sustitución y al método de integración por partes, una y otra vez.
P. Tenían razón mis amigos… la cosa se complica!
¡No, Paco! Se hace más laborioso, pero no más complejo. Lo interesante, insisto, no es la complejidad, es la posibilidad de aplicar simultáneamente los conceptos previos.
Empecemos y no dilatemos más nuestro trabajo ¿Recuerdas cómo se deriva un producto de funciones? Por ejemplo, f(x)g(x)
P. Si profe. La derivada de una función producto es igual a la derivada de la primera función multiplicada por la segunda función, mas la derivada de la segunda función multiplicada por la primera función.
Correcto Paco! Lo que dijiste en palabras es simbólicamente lo siguiente:

P. Bueno, si usted lo dice. Lo entiendo mejor con mis propias palabras
¿Qué pasa Paco? Te noto un poco extraño ¿no quieres que sigamos con nuestro estudio de integrales?
P. Que pena profe! Tiene razón, no estoy concentrado. Tengo mi cabeza en otros problemas, precisamente no de integrales
Todos los tenemos. Trata de dejarlos a un lado mientras trabajamos. Igual no los vas a solucionar enojándote conmigo.
P. Tiene razón profe. Sigamos con nuestro trabajo.
Ok! Paco. En la expresión anterior vamos a integrar en ambos miembros de la igualdad

En el primer miembro tenemos la integral de la derivada, por ser inversas podemos escribir:
P. ¡Que bien profe! Ahora si me estoy motivando, adiós a los otros problemas
Por el momento Paco. Ahora hagamos una transformación de términos:


Esta es la famosa fórmula para integrar por partes

P. ¡Vaya formulita!
Esta fórmula Paco se puede expresar en otra forma. Supongamos que f(x) = u y g(x) = v, a qué sería igual du y dv?
P. Haber… du = f’(x)dx … dv = g’(x)dx… ¿es correcto?
Correcto Paco. Si reemplazamos en nuestra formulita, obtendríamos:

P. Más sencilla profe… así simplificada es más fácil de trabajar
No es más sencilla, es la misma fórmula expresada de otra forma. Su simplificación es sólo en la simbología utilizada.
Veamos un ejemplo empleando las dos formas. Vamos a resolver la siguiente integral:
P. Huy profe… son más sencillos mis problemas personales. Creo que me volveré a concentrar en ellos
No seas tan prevenido Paco. Antes de anticiparte a problemas inexistentes, concéntrate en la solución que le vamos a dar a esta integral
Una sugerencia inicial, es hacer f(x) igual a una de las expresiones de la integral de tal forma que su derivada sea una expresión más simple. Me explico, si eligiéramos f(x) = cos x, su derivada f´(x)=-sen x, no es una expresión más simple.
P. Ya profe, la cogí… hagamos f(x) = x, ya que su derivada f´(x) es igual a dx
Que bien Paco! Luego de seleccionar f(x), la otra expresión debe ser igual a g´(x). Es decir g´(x) = cos x dx ¿A qué es igual entonces g(x)?
P. La hallo integrando… la integral de cos x…. ya! g(x) = sen x
Muy bien Paco! Ya tenemos todas las expresiones de la formulita… reemplacemos
O sea:
¡Sencillo Paco!
P. Si señor. No era tan complejo como me lo dijeron
Juzga por tu experiencia, no por la de los demás! Miremos Paco que usando la otra forma, el procedimiento es igual. Te lo voy a explicar pos pasos:
Paso 1. Hagamos u = x (su derivada hace más simple la integral)
Paso 2. Hallamos du = dx
Paso 3. Hagamos dv = cos x
Paso 4. Hallamos v = sen x (integrando)
Paso 5. Reemplazamos en la formulita:

P. Tiene razón profe. Es lo mismo uno u otra forma de presentación. Créame que me ha servido esta sesión para despejar mi cabeza. Ahora atenderé mis otros problemas, los cuales son más simples. Hasta pronto profe.
Hasta la próxima Paco, te dejo el siguiente video para que lo observes en casa:


posted by Juan Guillermo Rivera Berrío at 15:48 0 comments

martes, 21 de agosto de 2007

Sesion 2

Que tal Paco ¿Trabajaste con los ejercicios propuestos?

P. Si profe, pero tengo tres inquietudes

¿Cuáles Paco?

P. La primera tiene que ver con el noveno ejercicio. Traté de hacerlo por sustitución pero me fue imposible ¿no será que le faltó alguna t, profe?

Sabía que, para algunos estudiantes, algún problema iba a presentar este ejercicio. No fuiste la excepción Paco. Recuerdas el mensaje de Alan Turing? No todos los problemas se pueden resolver, al menos con lo que sabemos. Sin embargo, este ejercicio tiene una solución inmediata.

P. Créame profe que le busqué por todos lados y no vi solución.

Y si te regresas a la última sesión de la Integral Indefinida?

P. Haber… Huy profe, que pena. Tiene razón… está en la tabal de integrales y es la número 14.

Te recuerdo la segunda frase de esa sesión: “Otra forma de hallar las primitivas de una función es recurriendo a una tabla de integrales”. Precisamente escogí ese ejercicio para que tuvieras que recurrir a esta herramienta, como una alternativa a tu problema.

P. Igual pude recurrir a un programa de cálculo simbólico.

Ojo Paco. Los programas de cálculo simbólico los vas a usar para verificar, no para resolver tus ejercicios. Por otra parte, la tabla de integrales que presentamos en la sesión seis del primer capítulo, las puedes utilizar como ayuda a la solución de ejercicios.

P. Comprendo profe. Volviendo a los programas, desde allí surge mi segunda inquietud. Tuve problemas con la sintaxis de algunas integrales, especialmente la raíz cuadrada.

Es razonable Paco. Debes leer con más detalle las ayudas que te brindan esto programas. Sin embargo, te presento a continuación la solución de algunos ejercicios en tres de dichos programas. Los tres aceptan la siguiente sintaxis para raíz cuadrada: SQRT(expresión), la siglas vienen de las consonantes (sin repetir) de “SQuare RooT” o “raíz cuadrada”.

Integrando con DERIVE

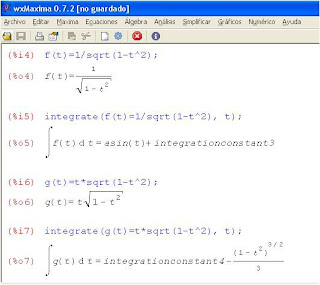
Se usa el comando INT(expresión, variable). Por ejemplo INT(1/sqrt(1-t^2),t) es el comando para integrar tu ejercicio problemático. En la siguiente imagen podrás observar la solución a tres de los ejercicios planteados. Al lado derecho aparece la solución. La respuesta que aparece como ASIN(t) es lo mismo que “ARCO SENO de t” o sen-1t.

Recuerda que debes incluir la constante de integración a cada solución

Integrando con MAXIMA

Maxima utiliza el comando integrate(función, variable). Observa en la imagen que la solución incluye la constante de integración

Integrando con MatLab

Similar a DERIVE, utiliza el comando int(expresión, variable). Recuerda de iniciar con el comando syms var1 var2 var3… Donde var corresponde a las variables a ser utilizadas. Para el caso de nuestros ejercicios: x, t, n.


P. Genial esto de los programas de cálculo simbólico. Pero qué pasa con las integrales definidas? Hemos realizado sólo ejemplos con integrales indefinidas.

Tienes razón Paco. Por ello decidí dejar en un capítulo aparte las técnicas de integración. Estas técnicas sirven para los dos tipos de integrales que vimos en los capítulos anteriores.

Par el caso de las integrales definidas, el proceso es el mismo con una excepción. Al cambiar las variables por sustitución, debes tener cuidado con los límites de integración. Con los siguientes ejemplos lo comprenderás:

Ejemplo 3.1.3

Espera Paco. Es aquí donde debes tener cuidado con los límites de integración. Tu proceso de integración está correcto hasta que escribiste la última expresión, la cual no es correcta. Te explico:

Los límites inferior y superior, 2 y 7 respectivamente, son para la función cuya variable es x. Al hacer el cambio de variable 2 + x por u, es fácil que me respondas la siguiente pregunta: Si x = 2 o x = 7 ¿a qué es igual u?

P. Entiendo. Los nuevos límites de integración son 4 y 9.

Puedes verificarlo por ejemplo en Maxima así:

integrate(f(x)=sqrt(2+x),x,2,7)

Vamos a un último ejemplo:

Ahora puedes practicar con los siguientes ejercicios:


Ejercicios 9. Calcular



posted by Juan Guillermo Rivera Berrío at 8:38 0 comments

jueves, 16 de agosto de 2007

Sesion 1

3. TÉCNICAS DE INTEGRACIÓN


Puedes descargar este capítulo aquí


P. ¿Cómo está profe? Le cuento que he consultado algunos libros de Cálculo y me encontré con ejercicios de integral definida y otros de integral indefinida que no pude resolver. Intenté por todos lados y nada. Bueno, excepto MatLab o Maxima.

Hola Paco! Tienes alguno de esos ejercicios a la mano

P. Claro. Por ejemplo:

P. Ok! Paco. Una de las enseñanzas que te deja tu exploración a otras fuentes de información (libros por ejemplo) es que tu formación aún es incompleta y que no puedes resolver todos los problemas y ejercicios que se presentan en Cálculo Integral. Otra enseñanza es que debes saber discernir entre lo que puedes resolver y lo que, por tu “incompletud”, no puedes

P. ¿Incompletud? Qué es eso profe

Disculpa Paco. Me vino a la memoria un teorema de un lógico de principios del siglo pasado, el teorema de incompletud de Gödel. Este teorema motivó a Alan Turing a estudiar qué funciones eran susceptibles de poder ser calculadas y cuáles no.

Pero dejemos a un lado esta divagación y como hacen los dermatólogos, vamos al grano.

P. Que chiste tan malo. Usted siempre tan descachado

Está bien Paco. Concentrémonos ¿Recuerdas la regla de la cadena?

P. Si profe. Esa regla la usamos para derivar funciones compuestas. Usted nos decía que derivábamos la función externa y la multiplicábamos por la derivada de la función interna ¿correcto?

Muy bien Paco, como alumno haces que mi labor no sea en vano. Lo que expresaste en palabras lo escribíamos así:

¿Cuál es f(g(x)) y cuál g(x)?


Huy profe! Que teso es usted, me dio la función que quería integrar. Eso quiere decir que la integral de mi ejercicio es precisamente la función compuesta que derivé. Humm… pero cómo hago para adivinar esa función compuesta?

Excelente Paco. Estás pensando con profundidad. Ahora déjame ayudarte con una de las llamadas técnicas de integración. Para este primer caso usaremos una de ellas, la cual es aplicable en funciones cuya primitiva es precisamente una función compuesta

3.1 Regla de sustitución

De acuerdo al ejercicio anterior, podemos enunciar el siguiente teorema:

Teorema 10. Regla de la cadena para antiderivación

Sea g una función derivable y se el contradominio de g algún intervalo I. Suponga que f es una función definida en I y que F es una primitiva de f en I, entonces

Observa y dime cuál es g(x), g´(x) y cuál es f(g(x))?

P. Comprendo profe el truco. g(x)= x2 +1, g´(x)= 2x y f(g(x)) = (x2 + 1)1/2

Muy bien Paco. Ahora según el teorema dy/dx = 2/3(x2 + 1)3/2 + c

Sencillo Paco, no hay truco. Sólo una buena observación para identificar las funciones de la función compuesta y sus derivadas

Pero si quieres trucos, vamos a utilizar uno de ellos denominado regla de sustitución o de cambio de variables, veamos:

Primero. Cambia g(x) por la variable u. Es decir u = x2 + 1

Segundo. Deriva implícitamente en ambos extremos de la ecuación. Es decir du = 2xdx

Tercero. Sustituye en la integral que vas a calcular. Es decir:

Puedes integrar la integral obtenida Paco?

P. Claro profe. El resultado es 2/3u3/2 + c

Vamos bien Paco

Cuarto. En la solución, vuelve a sustituir u por g(x)

P. Ya la pillé profe. Entonces me queda 2/3(x2 +1)3/2 + c. La solución que hayamos por el teorema anterior. Me gusta más este truco de cambio de variable o de sustitución.

En algunos casos es más directo el teorema. En el fondo, tanto el teorema como el truco son lo mismo. Este truco nos lleva a esta definción:

Definición 4. Regla de sustitución

Si u = g(x) es una función diferenciable en el rango I, y f es continua sobre I, entonces:

Bueno Paco, Desarrollaremos dos ejemplos más para que puedas afrontar los ejercicios propuestos en esta sesión, algunos de ellos requieren de trucos adicionales:

Ejemplo 3.1.1 Usa la regla de la cadena para integrar la siguiente expresión

En este ejemplo fíjate que si tomamos g(x) = 3x2 + 1, entonces g´(x) = 6x

P. Pero tenemos 5x, no funciona la regla de la cadena!

Y si reescribimos la expresión así:

P. Claro profe. Eso me pasa por ser tan apresurado

Has un esfuerzo mental y dime cual sería F(g(x))?

P. Haber… si tenemos 4 en el exponente era porque la primitiva tenía 5… pero… ya! Profe, la función primitiva tenía que ser: 1/6(3x2 + 1)5 + c.

Muy bien Paco. Veamos como sería con cambio de variable:

Sea u = 3x2 +1

Entonces du = 6x

P. Tiene razón profe, con la regla de la cadena no fue tan complicado

Veamos otro ejemplo

Ejemplo 3.1.2. Dime Paco cómo resolverías esta integral?

P. Humm…No profe, ahí si me corchó. Por mucho esfuerzo mental que haga no veo la solución

Quizá te rendiste antes de luchar. Intentemos con cambio de variable

Ahora si, resuélvela


Muy bien Paco, al sustituir nuevamente te da esta solución:

P. Tiene razón profe. No era tan complicado

Ok! Paco, ahora estás preparado para resolver mas integrales

Ejercicios 8. Del libro Calculus de Gilbert Strang, el cual puedes bajar en http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm, he seleccionado los siguientes ejercicios:



posted by Juan Guillermo Rivera Berrío at 15:31 0 comments